用勾股定理证明海伦公式
使用Pandoc，渲染较慢，如果看到未渲染的页面，请稍等一下
如图：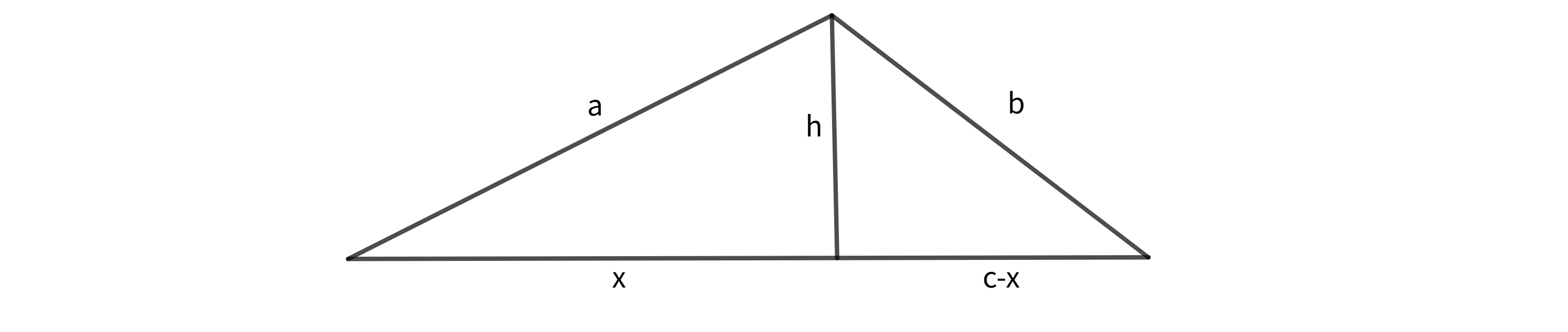 
$$
\begin{aligned}
h^2=a^2-x^2&=b^2-(c-x)^2\\
a^2-x^2&=b^2-(c-x)^2\\
a^2-x^2&=b^2-(c^2-2cx+x^2)\\
a^2-x^2&=b^2-c^2+2cx-x^2\\
a^2&=b^2-c^2+2cx\\
2cx&=a^2-b^2+c^2\\
x&=\frac{a^2-b^2+c^2}{2c}\\
\end{aligned}
$$
$$ \begin{aligned} h^2 &=a^2-x^2 \\ &=a^2-(\frac{a^2-b^2+c^2}{2c})^2\\ &=(a+\frac{a^2-b^2+c^2}{2c})(a-\frac{a^2-b^2+c^2}{2c})\\ &=\frac{2ac+a^2-b^2+c^2}{2c}\times\frac{2ac-a^2+b^2-c^2}{2c}\\ &=\frac{(a+c)^2-b^2}{2c}\times\frac{b^2-(a^2-2ac+c^2)}{2c}\\ &=\frac{(a+c)^2-b^2}{2c}\times\frac{b^2-(a-c)^2}{2c}\\ &=\frac{(a+c+b)(a+c-b)}{2c}\times\frac{(b+a-c)(b-a+c)}{2c}\\ &=\frac{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}{4c^2} \end{aligned} $$
$$ \begin{aligned} h&=\sqrt{\frac{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}{4c^2}}\\ \therefore S=\frac{1}{2}ch&=\frac{1}{2}c\sqrt{\frac{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}{4c^2}}\\ &=\sqrt{\frac{1}{4}c^2\times\frac{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}{4c^2}}\\ &=\sqrt{\frac{(a+c+b)(a+c-b)(b+a-c)(b-a+c)}{16}}\\ &=\sqrt{\frac{a+c+b}{2}\times\frac{a+c-b}{2}\times\frac{b+a-c}{2}\times\frac{b-a+c}{2}}\\ &=\sqrt{\frac{a+b+c}{2}\times\frac{a-b+c}{2}\times\frac{a+b-c}{2}\times\frac{b-a+c}{2}}\\ \end{aligned} $$ $$\text{设}p=\frac{a+b+c}{2}，则\frac{a-b+c}{2}=p-\frac{2b}{2}=p-b$$
$$以此类推 \frac{a+b-c}{2}=p-c \frac{b-a+c}{2}=p-a$$
$$\therefore S=\sqrt{p(p-a)(p-b)(p-c)}$$